Vous êtes ici
Filtrer les actualités par :

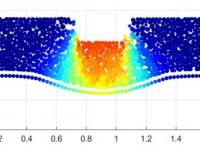
" Études expérimentale et numérique des plateformes granulaires renforcées par géosynthétiques sur sol mou " le 4 Avril à 14h (Amphithéâtre Ouest des Humanités)

Equipes de recherche -
08/03/2024
Perte de portance dans les structures poteau/poutre en béton armé: premier essai à échelle réelle réussi!



